30 60 90 Triangle Definition Theorem Formula Examples
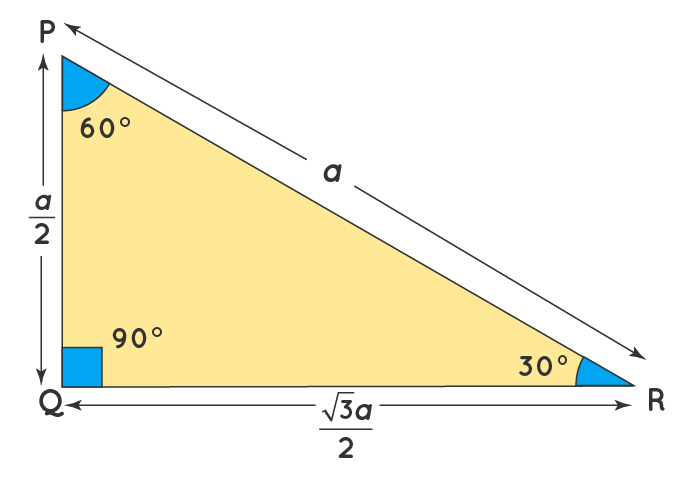
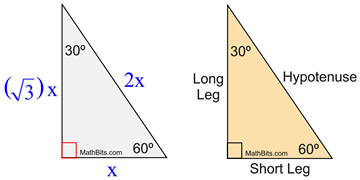
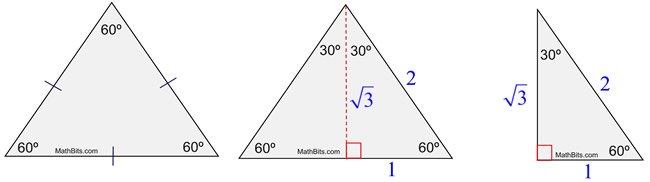
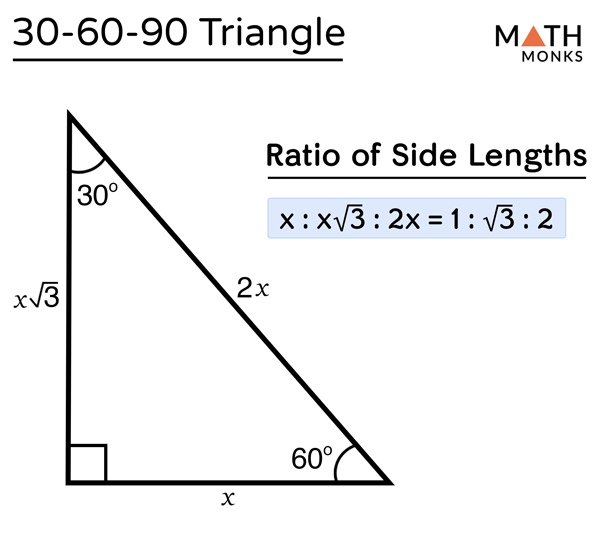
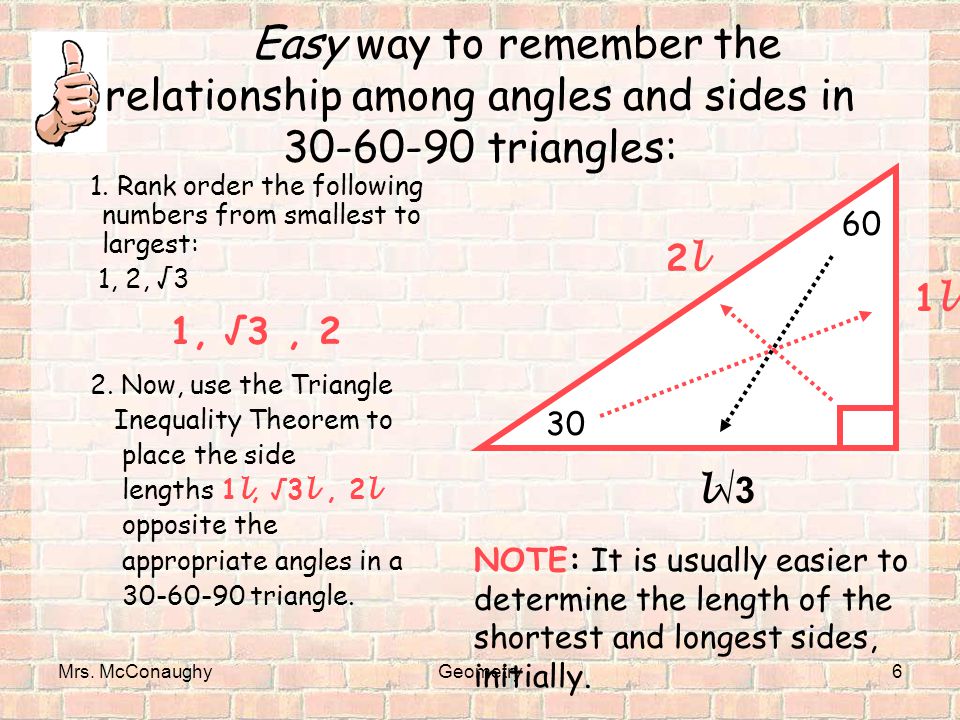
30°60°90° Triangles The measures of the sides are x, x√3, and 2xIn a 30°−60°−90° triangle, the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is √3 times the length of the shorter legA triangle is a special right triangle The other type of special right triangle is These numbers represent the degree measures of the angles The reason these triangles are considered special is because of the ratios of their sides they are always the same!
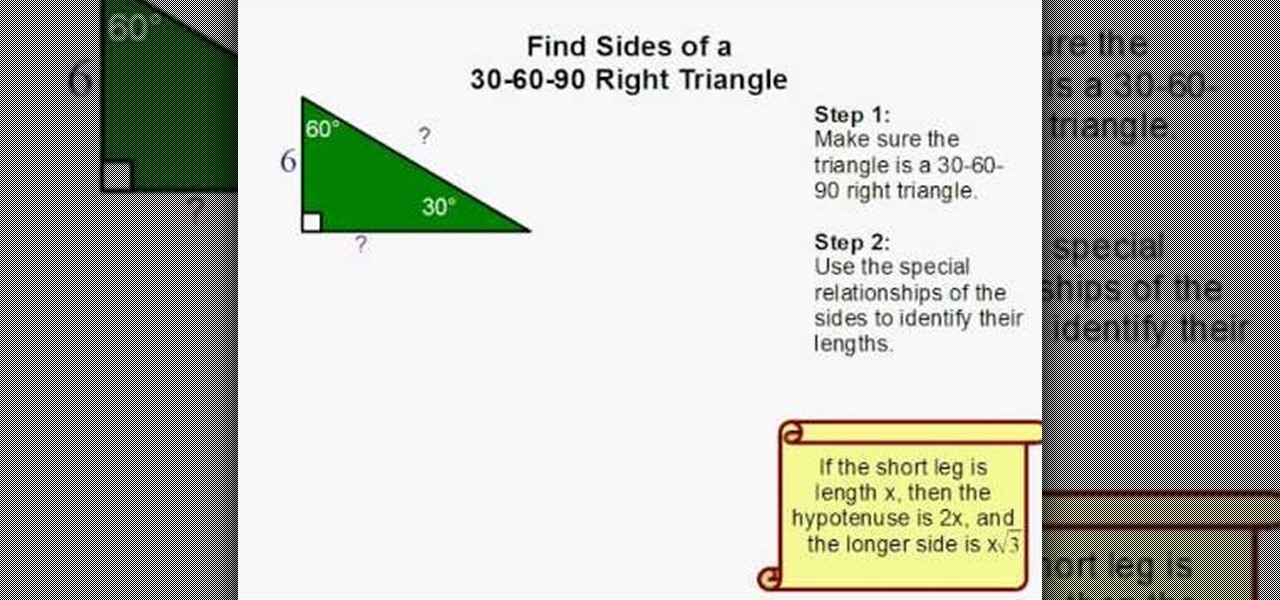
30 60 90 triangle solve for sides
30 60 90 triangle solve for sides-45°45°90° triangle The 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90° triangle, knowing one side length allows you to determine theThe triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and solutions on how to use
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
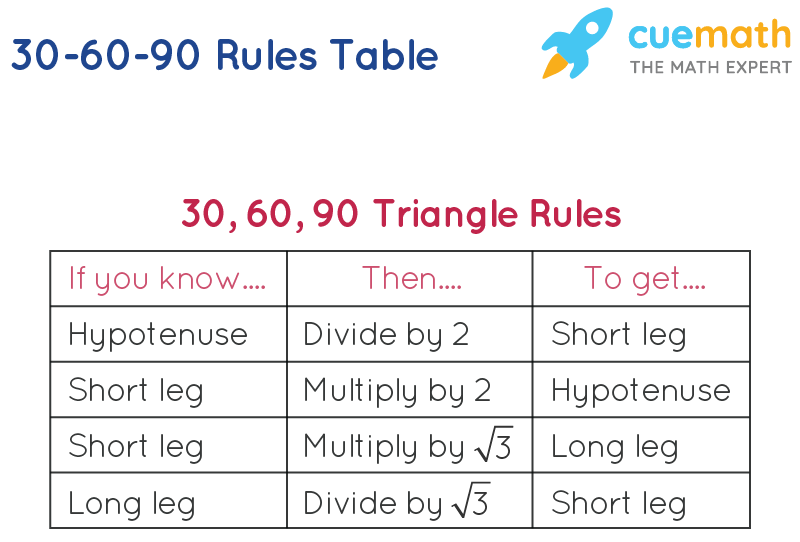
We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a2b2=c2 12(3–√)2=13=4=c2 4–√=2=c Using property 3, we know that all triangles are similar and their sides will be in the same ratio In a triangle, the ratio of the sides is always in the ratio of 1√3 2 This is also known as the triangle formula for sides yy√32y Let us learn the derivation of this ratio in the triangle proof section How do you find the side lengths of a 30 60 90 Triangle?
THE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that below The side opposite to the right angle is called the hypotenuse (side c in the figure) The sides adjacent to the right angle are called legs (or catheti, singular cathetus) What is the formula for area right triangle? In a triangle, the ratio of the sides is always in the ratio of 1√3 2 This is also known as the triangle formula for sides yy√32y Let us learn the derivation of this ratio in the triangle proof section What are the rules of a 30 60 90 right triangle?
30 60 90 triangle solve for sidesのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons | 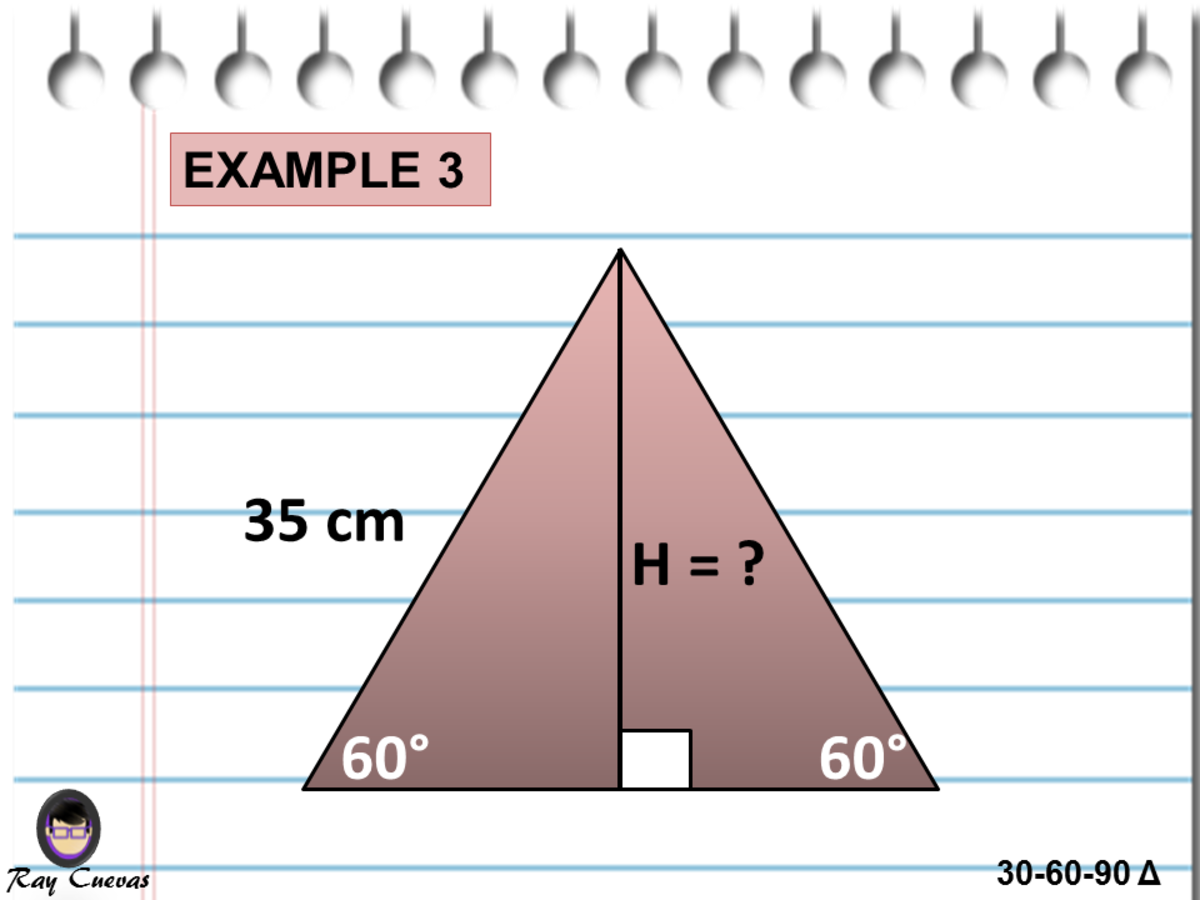 File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons | File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
「30 60 90 triangle solve for sides」の画像ギャラリー、詳細は各画像をクリックしてください。
 File 30 60 90 Triangle Svg Wikimedia Commons | 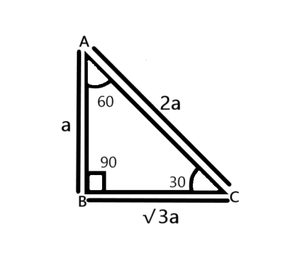 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons | 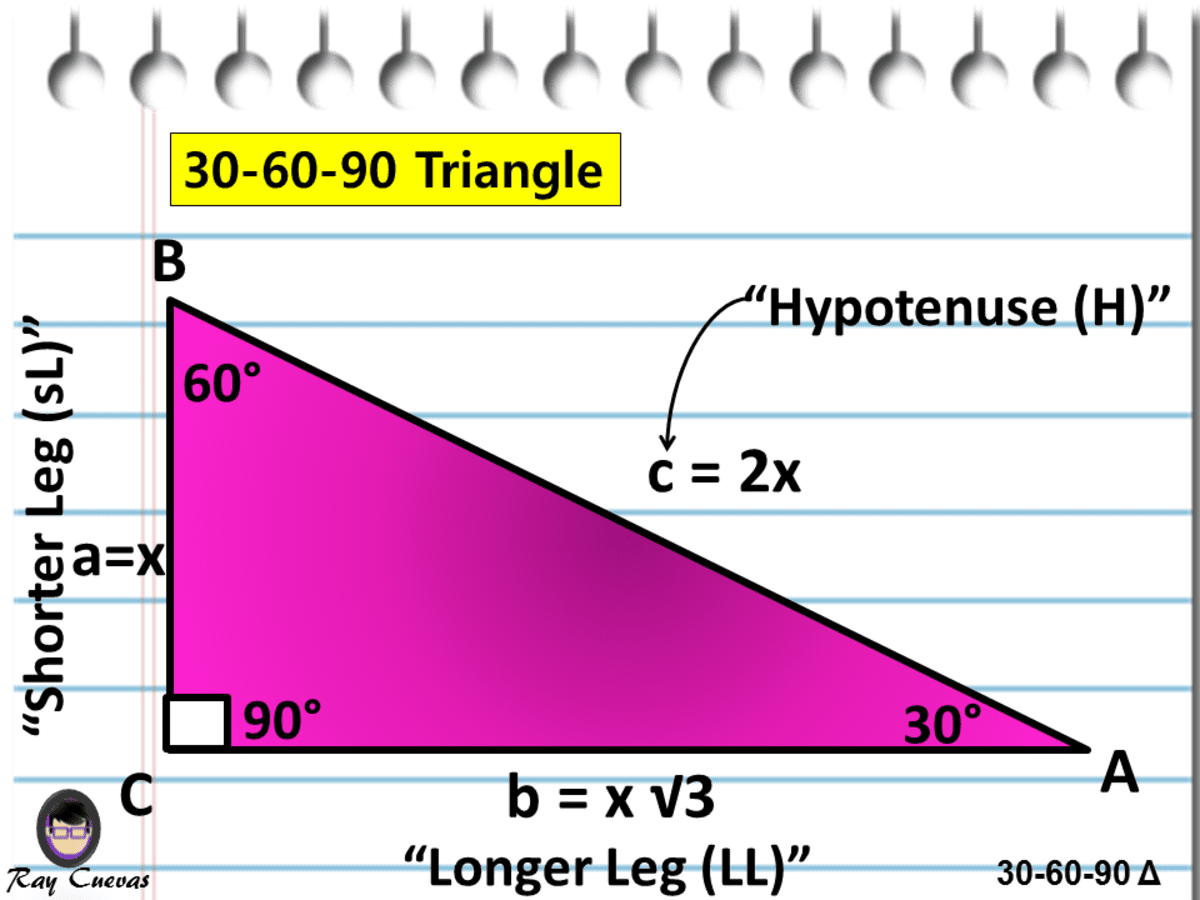 File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
「30 60 90 triangle solve for sides」の画像ギャラリー、詳細は各画像をクリックしてください。
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons | File 30 60 90 Triangle Svg Wikimedia Commons | 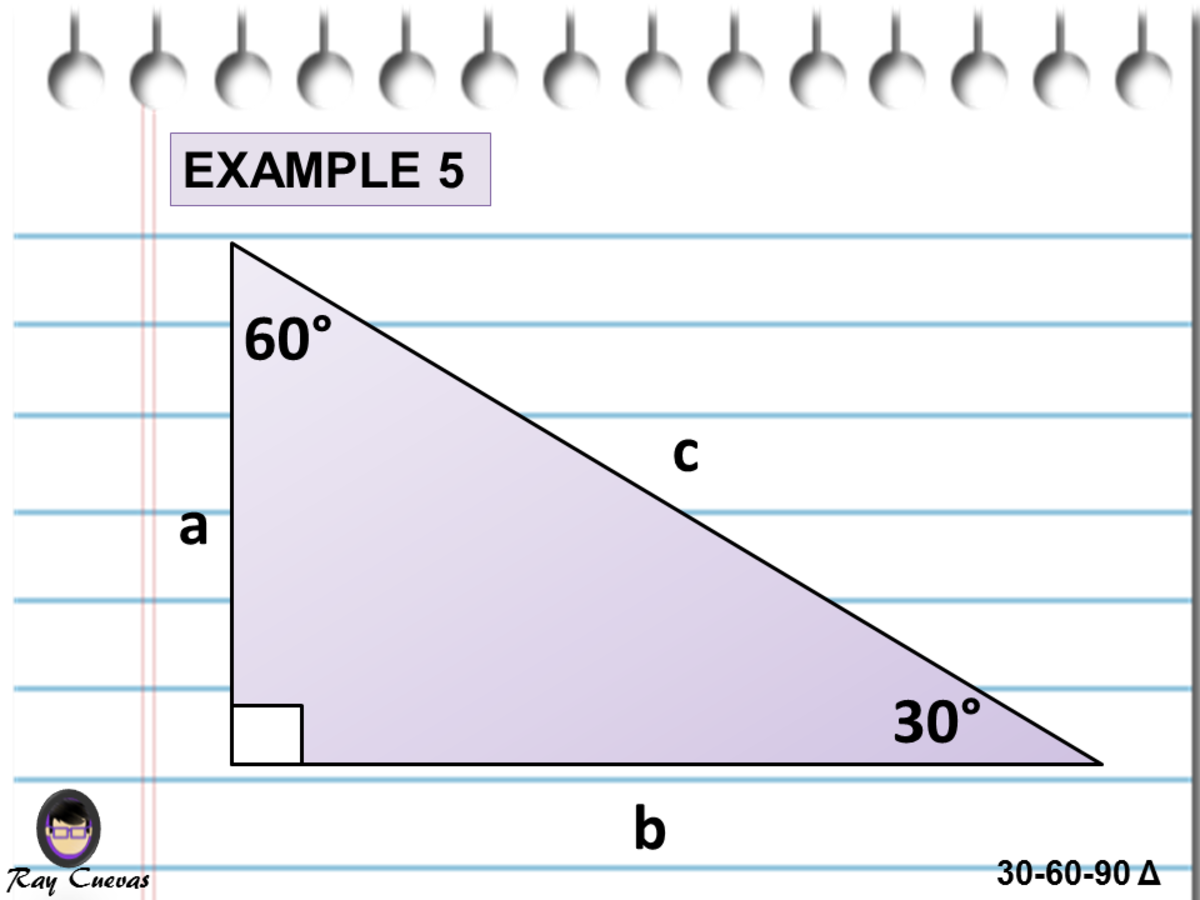 File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
「30 60 90 triangle solve for sides」の画像ギャラリー、詳細は各画像をクリックしてください。
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |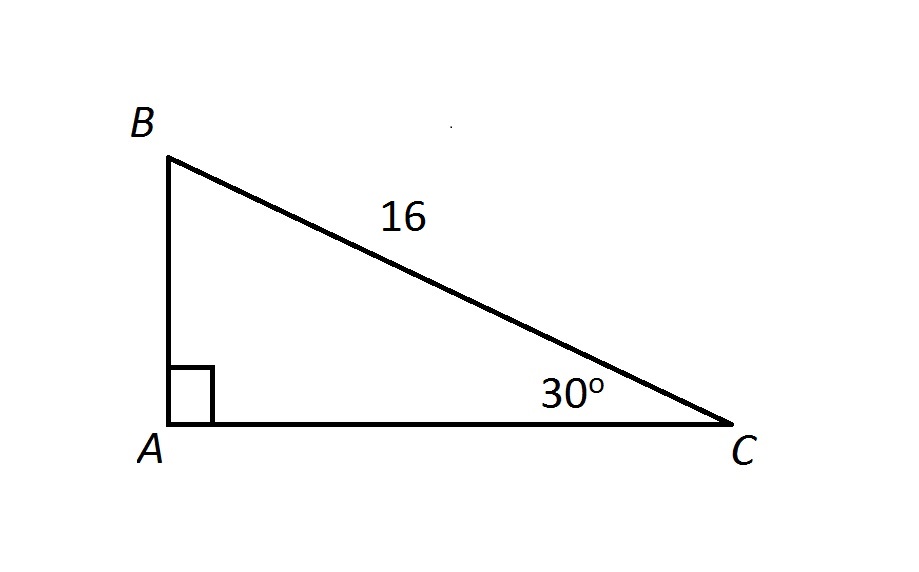
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |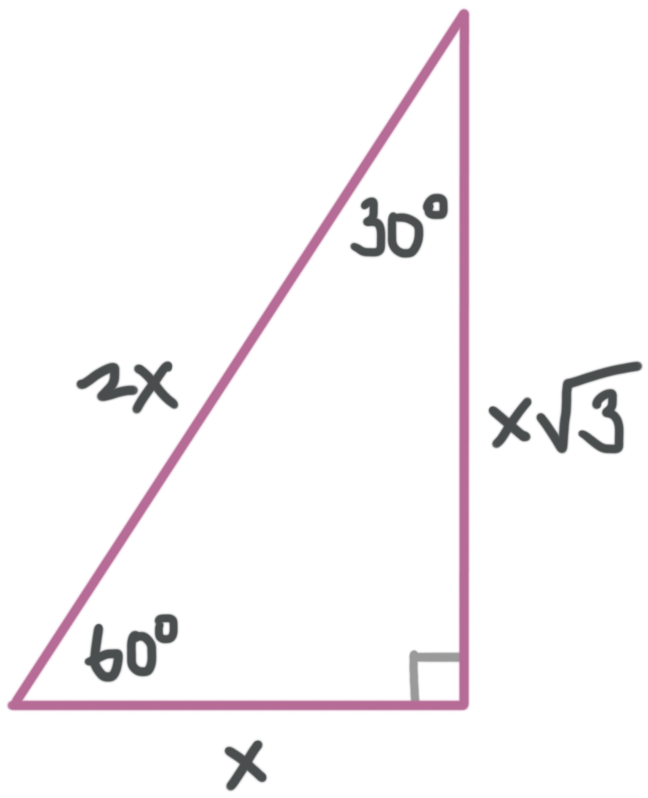
 File 30 60 90 Triangle Svg Wikimedia Commons | File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
「30 60 90 triangle solve for sides」の画像ギャラリー、詳細は各画像をクリックしてください。
 File 30 60 90 Triangle Svg Wikimedia Commons | File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
「30 60 90 triangle solve for sides」の画像ギャラリー、詳細は各画像をクリックしてください。
 File 30 60 90 Triangle Svg Wikimedia Commons | 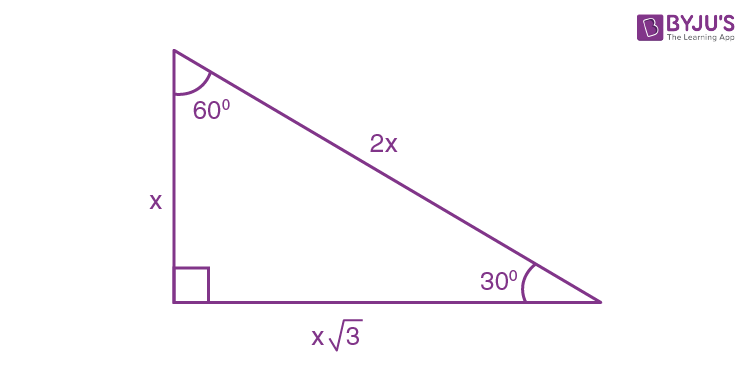 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons | 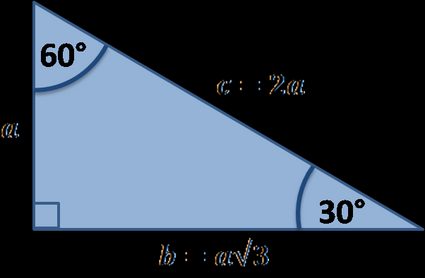 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
「30 60 90 triangle solve for sides」の画像ギャラリー、詳細は各画像をクリックしてください。
 File 30 60 90 Triangle Svg Wikimedia Commons | 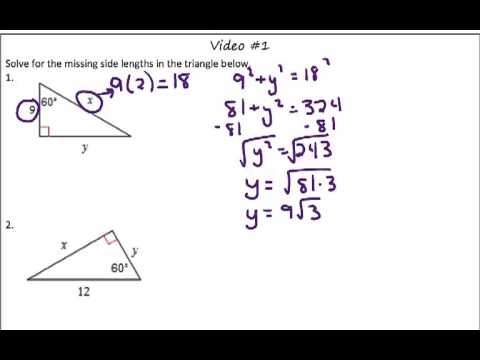 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
「30 60 90 triangle solve for sides」の画像ギャラリー、詳細は各画像をクリックしてください。
 File 30 60 90 Triangle Svg Wikimedia Commons | 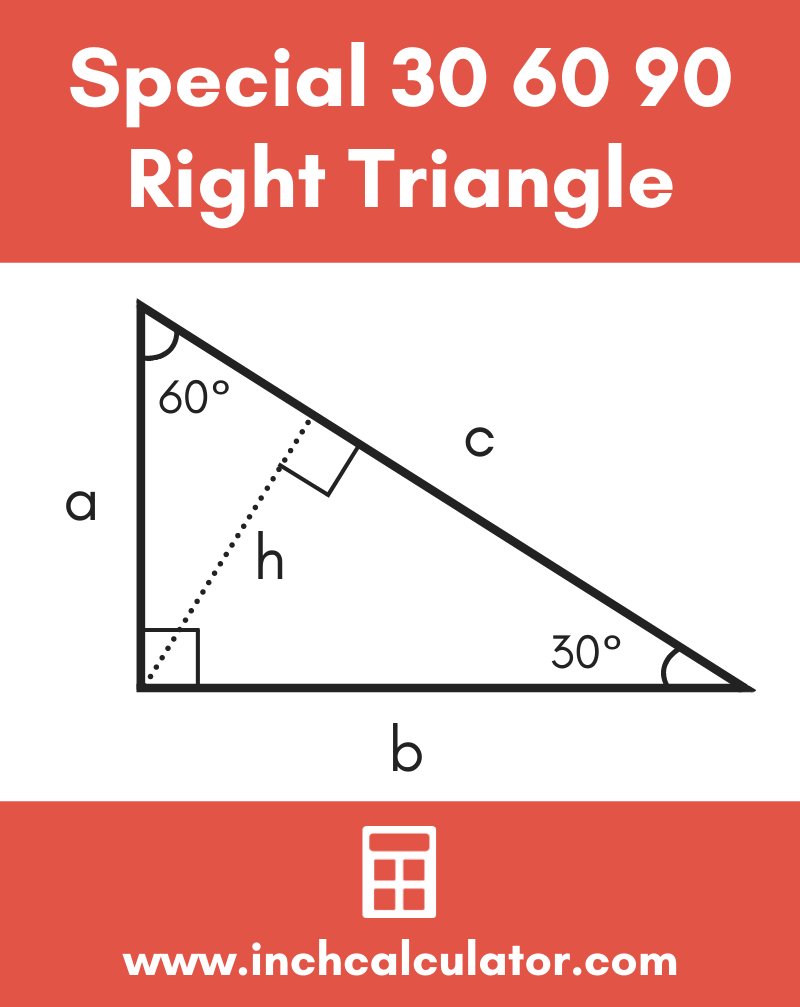 File 30 60 90 Triangle Svg Wikimedia Commons | File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons | 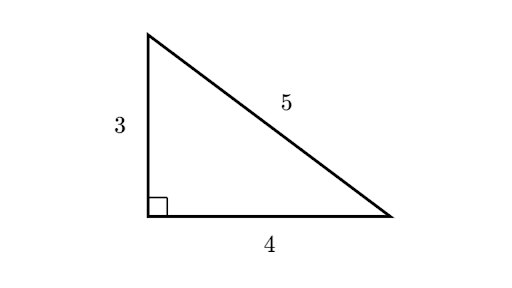 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
「30 60 90 triangle solve for sides」の画像ギャラリー、詳細は各画像をクリックしてください。
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons | File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
「30 60 90 triangle solve for sides」の画像ギャラリー、詳細は各画像をクリックしてください。
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons | 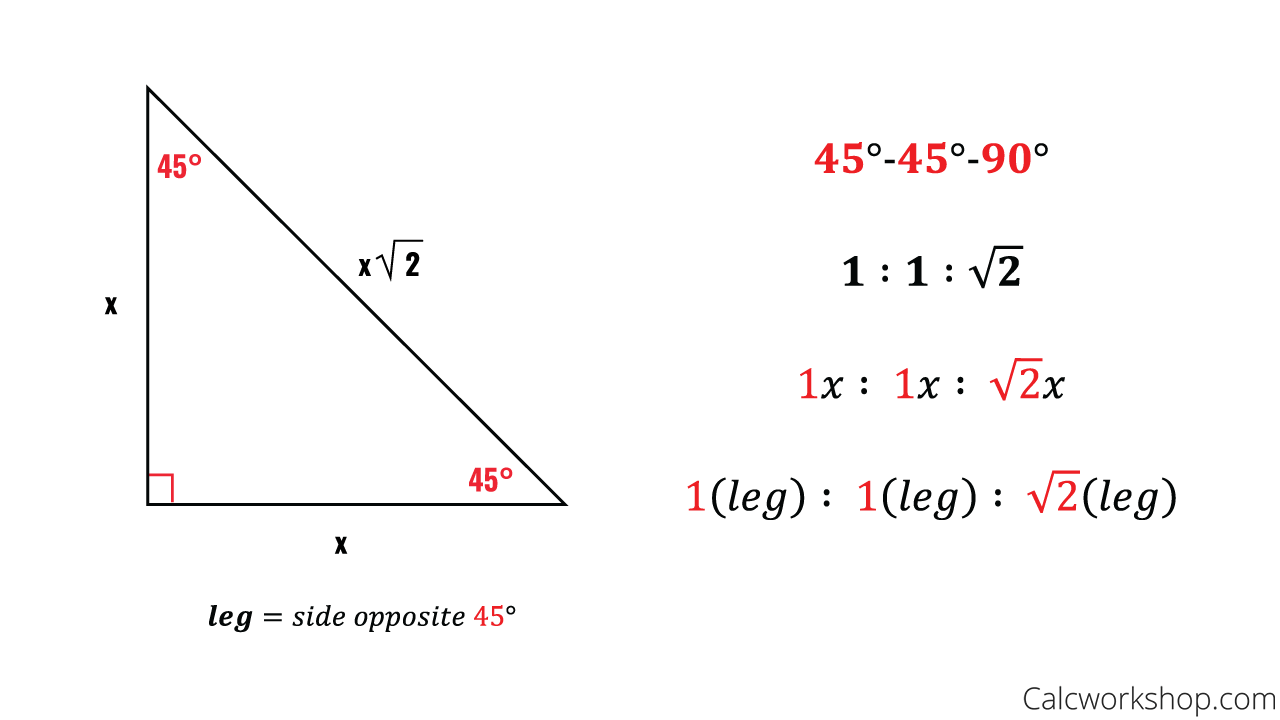 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
「30 60 90 triangle solve for sides」の画像ギャラリー、詳細は各画像をクリックしてください。
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
「30 60 90 triangle solve for sides」の画像ギャラリー、詳細は各画像をクリックしてください。
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
 File 30 60 90 Triangle Svg Wikimedia Commons |  File 30 60 90 Triangle Svg Wikimedia Commons |
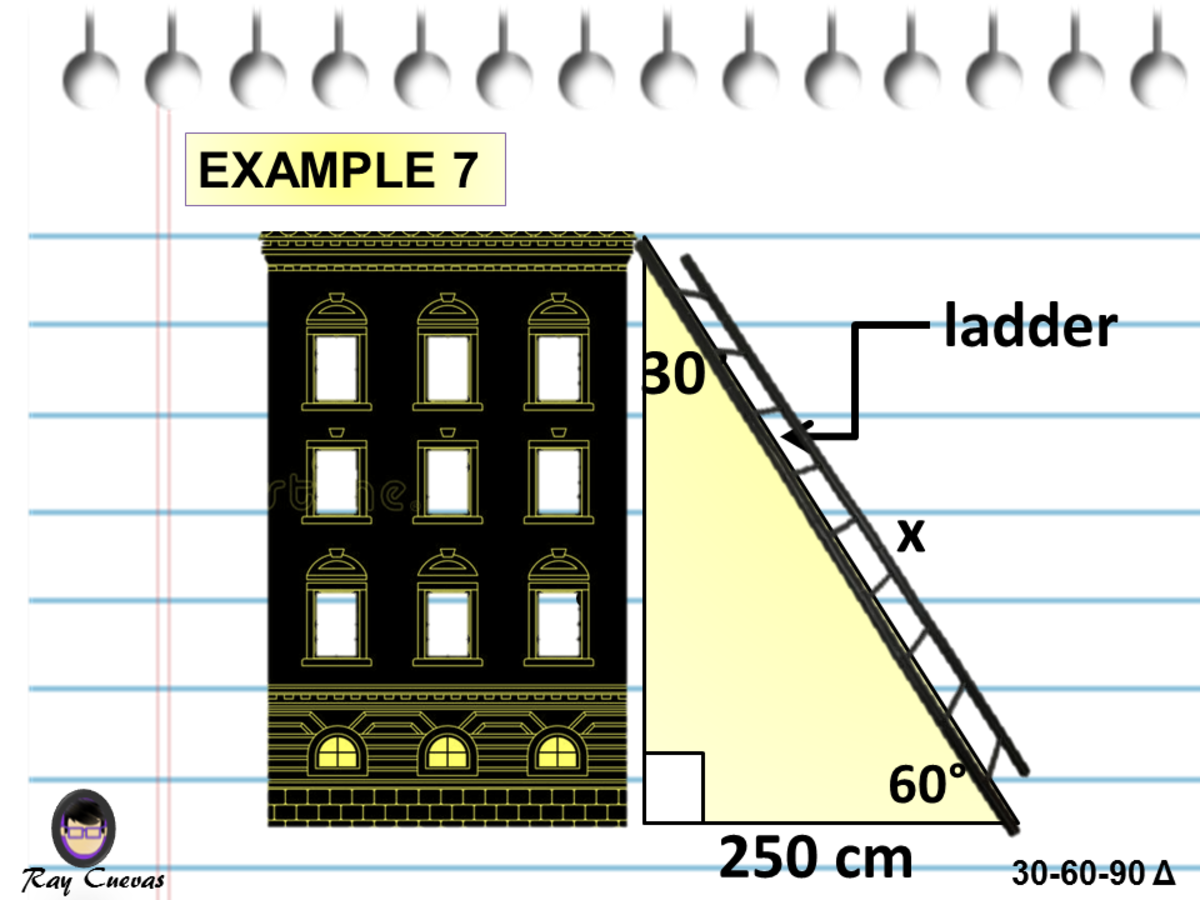
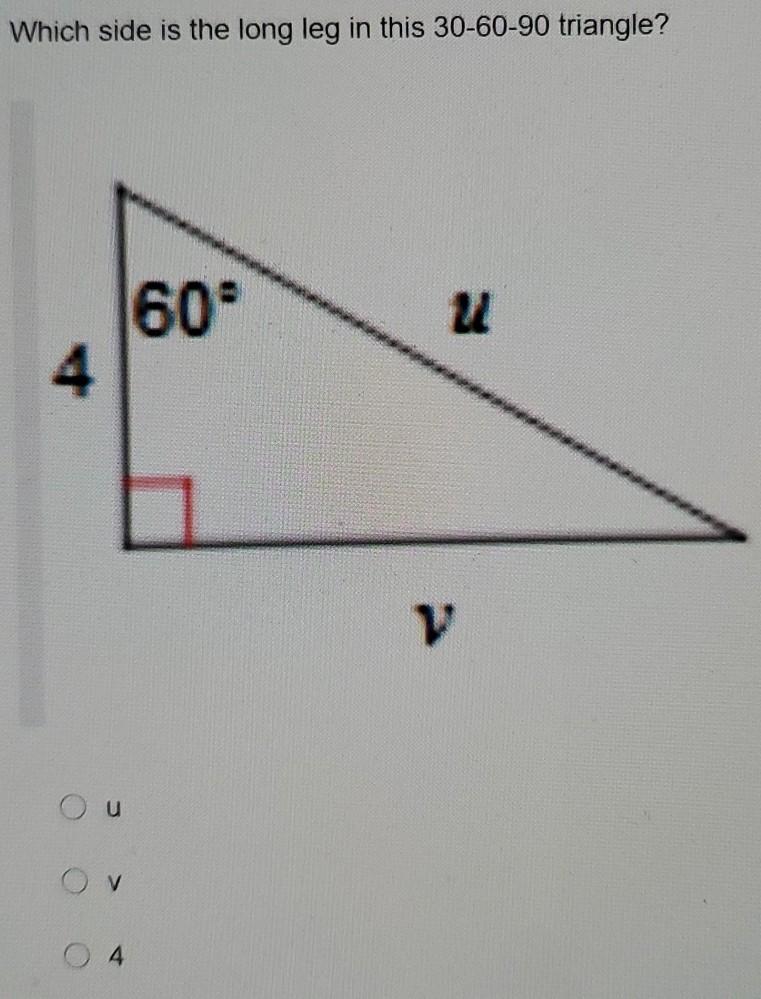
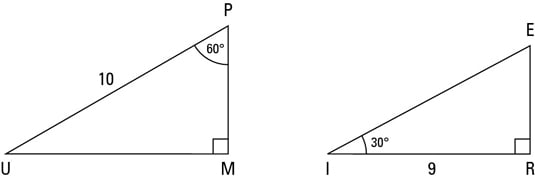
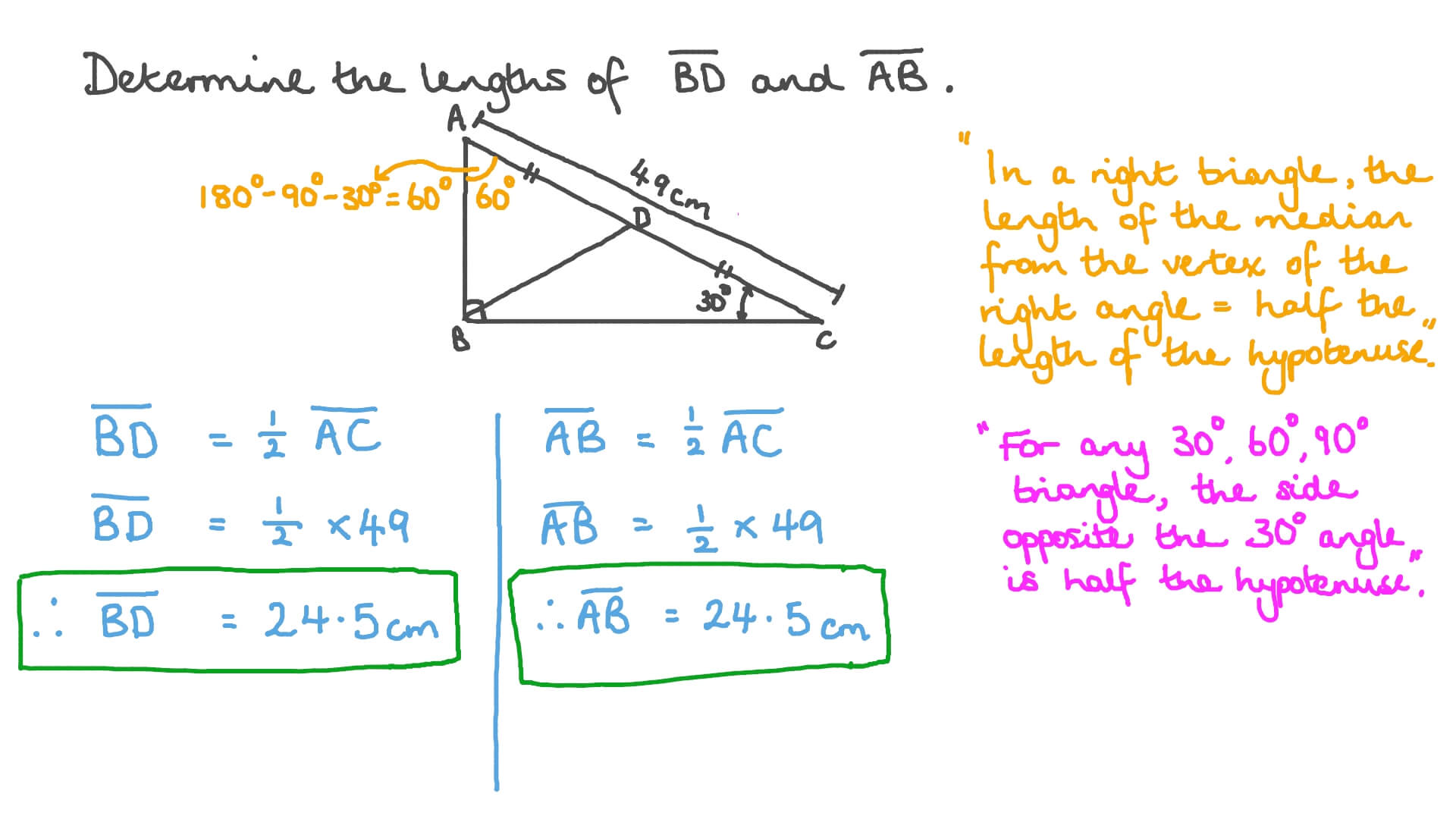
Which side of 30 60 90 triangle is which?30 60 90 triangle formula for sides Example Problems To see the in action, we've included a few problems that can be quickly solved with this special right triangle Sample Geometry Problem If one angle of a right triangle is 30º and the measure of the shortest side is 7
Incoming Term: 30 60 90 triangle formula for sides, 30 60 90 triangle solve for sides,
0 件のコメント:
コメントを投稿